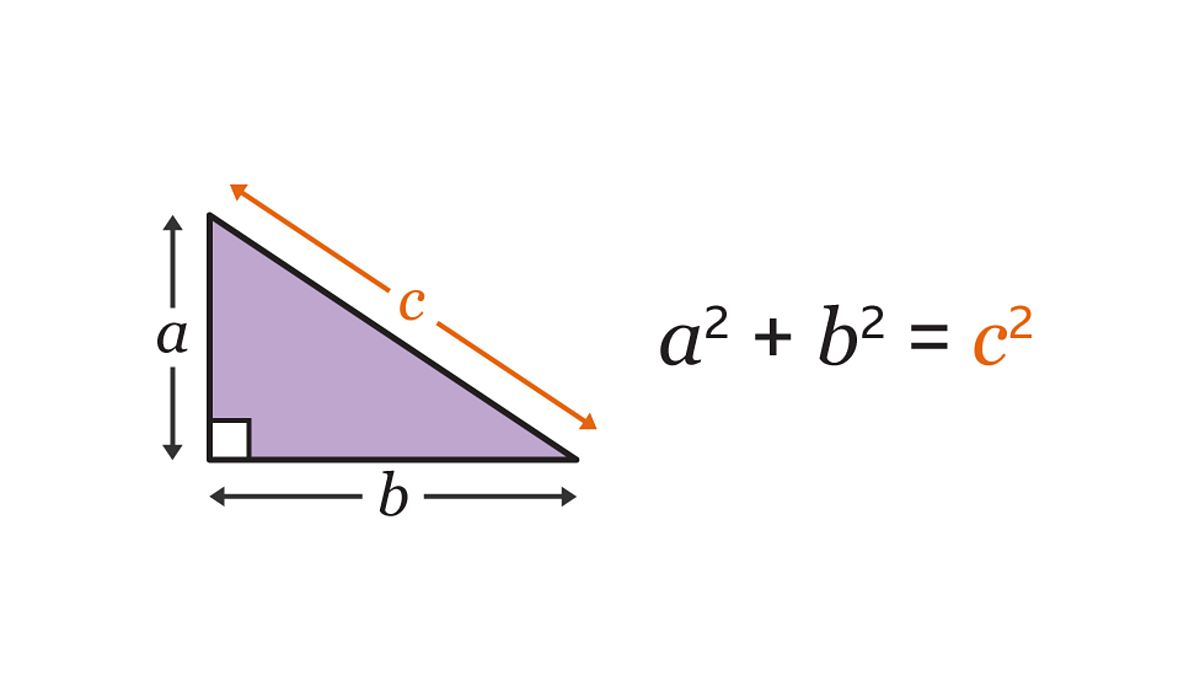Pythagorean and Thales Theorems

I’m still on geometry because I want to cover more basic contents that are related to graphics. If you know something from scratch, or just the base knowledge, you are able to do deal better with complexity in higher levels of abstraction. If you don’t care about it, go away ~~(straight to hell)~~.

pythagorean Theorem

This theorem is applied to right-triangles (triangles that has one of its angles with 90 degrees). Basically, the sum of the squares of the legs are equal of the length of the hypotenuse. The hypotenuse is the opposite side of the right angle.

The formula tell us:

\[c^2 = a^2 + b^2\]

Where:

\(a\) and \(b\) are the length of the legs
\(c\) is the length of the hypotenuse

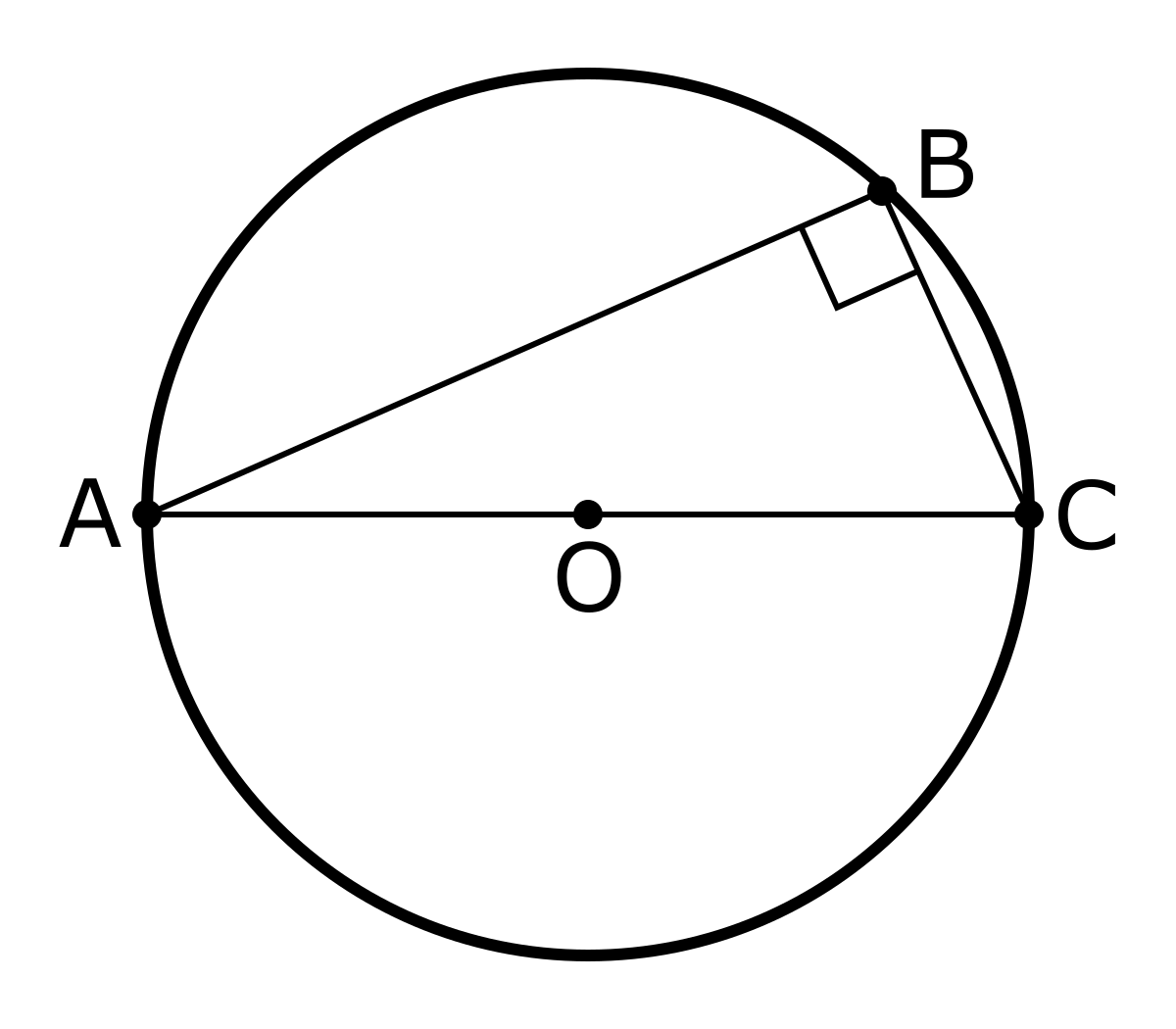
Thales’ Theorem

Thales’ Theorem, describes the proportionality of line segments when two transversals intersect several parallel lines. If two transversals intersect a set of parallel lines, then the segments formed on the transversals are proportional.

In simpler terms, if two transversals \(AB\) and \(CD\) cut through parallel lines \(r\), \(s\), and \(t\), the following relationship holds:

\(\frac{A_1B_1}{A_2B_2} = \frac{C_1D_1}{C_2D_2}\)

Where:

\(A_1 B_1\) and \(A_2B_2\) are segments on one transversal,
\(C_1D_1\) and \(C_2D_2\) are the corresponding segments on the other transversal.

It is also applied in triangles: if a line parallel to one side of a triangle intersects the other two sides, it divides them proportionally, forming a smaller triangle that is similar to the original. This is congruence! (I’ve already talked about this in my previous posts.)

Thanks, bye!

References

All credits to the original sources for the images used in this document.